Graph Algorithms as a Detective Story

It was a peaceful evening when disaster struck—your cat, Whiskers, went missing! 🐾

As the top detective in the neighborhood, it’s your job to track him down. But where do you even start? There are so many possible hiding spots—your backyard, the neighbor’s house, the park, or even the cafe down the street.

Finding Whiskers might seem overwhelming, but this is where graph algorithms come in! Just like solving a mystery, these algorithms help us navigate different locations (nodes) and paths (edges) to determine the best way to find our missing cat.

Let’s crack the case!

Step 1: Mapping the Crime Scene 🗺️

Before we begin the search, we need a map of all possible places Whiskers might be.

Nodes (Locations)

🏠 Home

🌳 Backyard

🏡 Neighbor’s Yard

🌲 Park

☕ Cafe

🌿 Alley

🎄 Tree

Edges (Connections)

• Home ↔ Backyard
• Home ↔ Neighbor’s Yard
• Backyard ↔ Alley
• Neighbor’s Yard ↔ Park
• Park ↔ Tree
• Park ↔ Cafe
• Alley ↔ Cafe

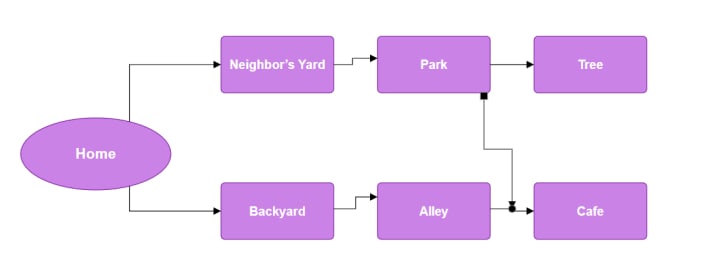
This forms a graph—a network of connected locations. Now, let’s use different search strategies to find Whiskers!

Step 2: Searching for Clues with Breadth-First Search (BFS) 🔍

The Strategy

BFS works like an organized neighborhood search. You start by checking the closest locations. If Whiskers isn’t there, you expand your search further.

How It Works

• Start at Home and check direct neighbors (Backyard, Neighbor’s Yard).
• If Whiskers isn’t there, check locations connected to them (Alley, Park).
• Keep expanding outward (Tree, Cafe) until you find him.

Why BFS is Useful

✅ Guarantees the shortest path in an unweighted graph.

✅ Ensures every location is checked systematically.

❌ Might take longer in large areas since it explores everything at the same depth first.

Think of it as asking every nearby person if they’ve seen Whiskers. If no one has, you expand the search radius until you find him!

Step 3: Exploring Deep with Depth-First Search (DFS) 🕵️‍♀️

The Strategy

DFS is different from BFS—it picks one direction and explores as deep as possible before backtracking.

How It Works

• Start at Home and choose one path (Backyard → Alley → Cafe).
• If Whiskers isn’t there, backtrack and explore another path (Neighbor’s Yard → Park → Tree).
• Keep searching until all possibilities are explored.

Why DFS is Useful

✅ Great for deep searches when Whiskers is far away.

✅ Uses less memory compared to BFS.

❌ Might take the wrong path first, making the search longer.

Think of it like following a single lead completely before considering alternatives. If you hear faint meowing in one direction, you might commit fully to checking that path first.

Step 4: Finding the Fastest Route with Dijkstra’s Algorithm 🚴‍♂️

The Strategy

You finally spot Whiskers—but he’s far away, stuck on a tree! Now, the challenge is getting there as quickly as possible.

Dijkstra’s Algorithm helps find the quickest route when travel times vary. Some paths may be shorter but slower (a narrow alley), while others may be longer but faster (a main road).

How It Works

• Start at Home and note the travel time to each location (2 minutes to Backyard, 5 minutes to Park).
• Always take the fastest option available at each step.
• Keep updating distances until reaching Whiskers.

Why Dijkstra’s is Useful

✅ Finds the fastest route when different paths have different travel times.

✅ Works well when you know distances between locations.

❌ Can be slower than BFS if all paths are equal.

If all routes took the same time, BFS would be enough. But when some roads are faster than others, Dijkstra’s ensures you don’t waste time on long detours.

Step 5: What If Whiskers Keeps Moving? (A* Algorithm) 🏃‍♂️

The Strategy

A* (A-Star) is like Dijkstra’s Algorithm—but smarter. Instead of blindly checking every possible path, it makes an educated guess about where Whiskers is most likely to be.

How It Works

• Instead of exploring all paths equally, A* prioritizes paths that seem more promising.
• It considers both distance and a hint (heuristic) about Whiskers’ behavior.
• If Whiskers loves high places, A* checks trees and rooftops first.

Why A is Useful*

✅ Faster than Dijkstra’s when you have good clues.

✅ Reduces unnecessary searches by making logical predictions.

❌ Might waste time if the clues are wrong.

If Whiskers usually hides under cars, you wouldn’t waste time checking rooftops first. A* lets you prioritize locations based on past behavior while still guaranteeing an efficient search.

Case Closed - What We Learned 🏆

After using these search strategies, you finally track down Whiskers—stuck on the cafe rooftop! 🎉

✅ BFS ensured you checked every possibility systematically.

✅ DFS helped explore deep hiding spots.

✅ Dijkstra’s Algorithm got you there in the shortest possible time.

✅ A* guided you to the most likely hiding spots first.

And just like that, mystery solved! Whether you're searching for a missing cat, navigating tangled city streets, or untangling a tricky problem, it's all about knowing which paths to take. 🔍🐾